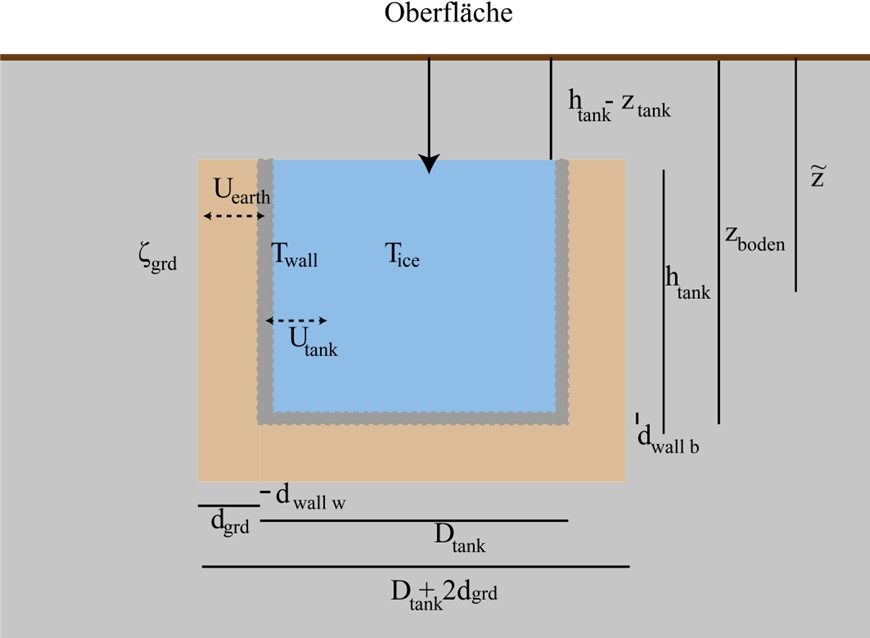
Modèle d’échange de chaleur avec le terrain
Paramètres
Le modèle de sol nécessite les paramètres suivants (Calc signifie qu’il est calculé en routine) :
| Paramètre | Description | Unité | Valeur |
| \(\widetilde{z}\) | Profondeur moyenne du réservoir de glace sous la surface du sol | m | Calc |
| Gt | Gradient géothermique | K/m | 0.03 |
| \(\rho_{grd}\) | Densité du sol | kg/m3 | 2’500 |
| cpgrd | Capacité thermique du sol | kJ/K | 800 |
| grd | Conductibilité thermique du sol | W/mK | 2 |
| Utank | Conductibilité thermique du réservoir | W/mK | Calc |
| Uearth | Conductibilité thermique de la terre | W/mK | Calc |
| V | Volume du réservoir de glace | m3 | 10 |
| zboden | Profondeur du fond du réservoir de glace | m | 3.2 |
| htank | Hauteur du réservoir de glace | m | 2.3 |
| Dtank | Diamètre du réservoir de glace | m | 2.7 |
| dgrd | Épaisseur de la couche de sol environnante | m | 0.5 |
| \(\overline{\theta_{e}}\) | Température extérieure moyenne | °C | 11 |
| \(\Delta\theta_{e}\) | Amplitude des fluctuations mensuelles de la température extérieure | °C | 9.3 |
| \(\lambda_{wall}\) | Conductibilité thermique de l’enveloppe du réservoir de glace | W/mK | 1.33 |
| dwall w | Épaisseur de l’enveloppe du réservoir de glace sur les côtés | m | 0.1 |
| dwall b | Épaisseur de l’enveloppe du réservoir de glace vers le bas | m | 0.12 |
Implémentation
La température du sol non perturbé est calculée en fonction de la profondeur dans le sol et du temps.
\(\ \zeta_{grd}(t,z) = \overline{\theta_{e}} – \Delta\theta_{e}\exp{\left( – \frac{z}{\delta_{grd}} \right)\cos\left\lbrack 2\pi\frac{\left( t – t_{shift} \right)}{t_{0}} – \frac{z}{\delta_{grd}} \right\rbrack} + G_{t}z\)
Où la profondeur de pénétration thermique est une mesure du retard de la température en profondeur par rapport à la température de surface. Il est calculé comme suit :
\(\delta_{grd} = \sqrt{\frac{t_{0} \cdot 3600\left\lbrack \frac{s}{h} \right\rbrack \cdot \lambda_{grd}}{\pi \cdot \rho_{grd} \cdot cp_{grd}}}\)
Pour z, on choisit la profondeur moyenne du réservoir de glace z̃ (\(\widetilde{z} = z_{boden} – 0.5 \cdot h_{tank}\)) et on suppose que la température du sol autour du réservoir est homogène.
Si le sol a une température différente de celle du réservoir de glace, un flux thermique se produit. Ainsi, la température de la paroi du réservoir de glace est calculée selon la formule :
\(T_{Wall} = \int\frac{1}{m_{grd}cp_{grd}}\left( UA_{earth}\left( \zeta_{grd} – T_{wall} \right) – UA_{tank}\left( T_{wall} – T_{ice} \right) \right)\mathbb{d}t\)
Où UAearth est le coefficient de transmission thermique de la strate de terre entre le sol non perturbé et la paroi du réservoir de glace. Il est calculé selon la formule :
\(UA_{earth} = \frac{\lambda_{grd}}{d_{grd}} \times \left\lbrack \pi\left( \frac{D_{tank} + 2d_{grd}}{2} \right)^{2} + \pi\left( D_{tank} + 2d_{grd} \right)\left( h_{tank} + d_{grd} \right) \right\rbrack\)
UAtank est le coefficient de transmission thermique de l’envoloppe du réservoir de glace et est calculé à partir de la surface du paroi ou du sol divisée par la résistance de transmission thermique respective. Dans ce modèle, l’échange thermique entre le réservoir de glace et le sol est limité à la partie inférieure et cylindrique du réservoir de glace. Les rendements/pertes thermiques via le couvercle conique ne sont pas pris en compte.
\(UA_{tank} = \frac{\left( \frac{D_{tank}}{2} \right)^{2}\pi}{\frac{d_{wall\ b}}{\lambda_{wall}}} + \frac{D_{tank\ }\pi\ h_{tank}}{\frac{\mathbb{d}_{wall\ w}}{\lambda_{wall}}}\)
mgrd est calculé à partir du volume de la strate de terre multiplié par sa densité – le volume est calculé à partir de la surface extérieure du réservoir de glace et de l’épaisseur de la strate de terre.