Estimation de la durée de vie
Le Return of Investment d’une batterie dépend de sa durée de vie. Cela dépend de la sollicitation de la batterie (durée de vie du cycle) ainsi que du temps (durée de vie calendaire). La durée de vie du cycle peut être estimée en comptant le nombre de cycles (par exemple, avec la méthode « Rainflow Cycle Counting« ).
La durée de vie calendaire, ainsi que la relation entre la profondeur de cycle (profondeur de décharge ) et le nombre de cycles jusqu’à défaillance \(C_{F}\), est généralement spécifiée dans la fiche technique de la batterie (voir la figure suivante).
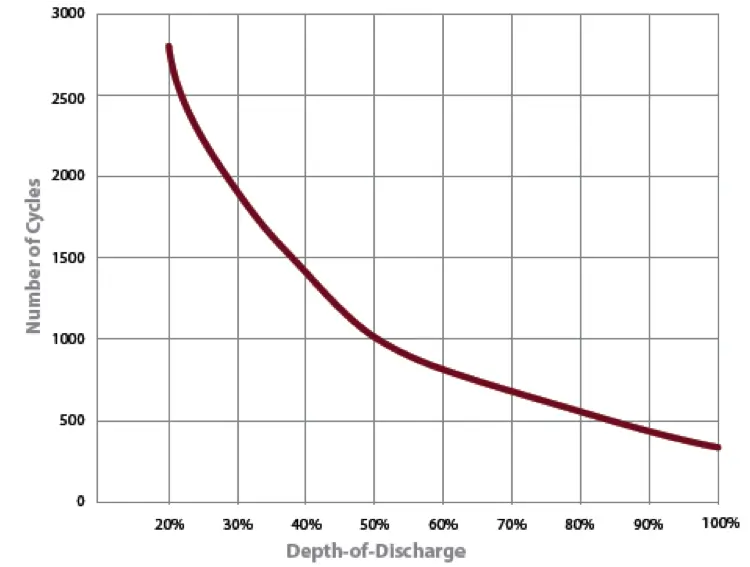
La relation entre le nombre de cycles jusqu’à la défaillance (number of cycles to failure) \(C_{F}\) et la profondeur de décharge (depth of discharge) est modélisée dans Polysun par l’une des deux fonctions suivantes :
- Comme une fonction exponentielle double (bien adaptée aux batteries au plomb)
\(C_{F} = \alpha_{1} + \alpha_{2} \cdot e^{- \alpha_{3} \cdot DoD} + \alpha_{4}{\cdot e}^{- \alpha_{5} \cdot DoD}\)
- Comme courbe de Wöhler (bien adaptée aux batteries lithium-ion)
\(C_{F} = \alpha_{1} \cdot DoD^{- \alpha_{2}}\)
Les paramètres \(\alpha_{1}\) à \(\alpha_{5}\) peuvent être fournis directement par le producteur de la batterie, ou bien ils peuvent être déterminés par régression non linéaire à partir du graphique de durée de vie des fiches techniques[1]. Tous les paramètres sont facultatifs. Cependant, s’ils sont manquants, aucune estimation de la durée de vie n’a lieu. Si seuls les paramètres \(\alpha_{1}\ \) et \(\alpha_{2}\ \) sont donnés, la courbe de Wöhler est automatiquement modélisée, sinon la fonction exponentielle double est utilisée.
Pour calculer la durée de vie des cycles dans Polysun, on utilise 20 bins ( Histogramm‑Bins) de même taille, qui comptent le nombre de cycles de la gamme \(DoD\) (Range) R correspondante. \(M_{i}\) est le nombre annuel de cycles avec la gamme \(R_{i}\). \(C_{FL,i}\) indique le nombre correspondant de cycles d’une gamme \(R_{i}\) jusqu’à la défaillance. A chaque cycle de la batterie, \({1/C}_{FL,i}\) de la durée de vie totale de la batterie est consommée. Le dommage annuel cumulé résulte de :
\(D = \sum_{i}^{}\frac{M_{i}}{C_{FL,i}\ }\)
Par exemple, si à la fin de la simulation D = 0.5, la moitié de la durée de vie de la batterie a été utilisée. En d’autres termes, la batterie doit être remplacée au bout de deux ans. Comme la durée de vie de la batterie dépend fortement des cycles de décharge profonde, seule une partie de la capacité disponible est utilisée pour les cycles quotidiens. La batterie n’est jamais déchargée plus profondément que \({SOC}_{\min}\). \(SOC \geq {SOC}_{\min}\) s’applique. Le \({SOC}_{\min}\) est spécifique au type et peut être trouvé dans les fiches techniques producteur.
Dans les résultats de simulation de la batterie, le nombre total de cycles effectués et les cycles profonds sont indiqués. Ce qui compte comme une décharge profonde est défini par le seuil de déchargement profond (deep cycle threshold) dans le dialogue des propriétés de la batterie.
La durée de vie totale \(L_{tot}\) de la batterie résulte du minimum de la durée de vie calendaire et de la durée de vie cyclique \(L_{cyc}\):
\(L_{tot} = \min{(L_{cal,\ }L_{cyc})}\)
Si aucune durée de vie calendaire n’est spécifiée dans l’entrée respective du catalogue de batteries, les valeurs suivantes sont supposées : 20 ans pour les batteries lithium-ion, vanadium redox flow et NiCd, ou 10 ans pour les batteries au plomb et NiMH.
[1] Par exemple, dans Excel, Matlab ou un outil en ligne comme zunzun.com