Formeln und Begriffe der Wirtschaftlichkeit
Netto-Barwert (NPV)
Der Netto-Barwert wird mit der Kapitalwertmethode ermittelt und ist international als Net Present Value (NPV) bekannt. Mit der Kapitalwertmethode werden alle Einnahmen und Ausgaben einer Anlage innerhalb der gewählten Betrachtungsperiode zinsbereinigt zusammengezählt. Die Zahlungsbeträge in den einzelnen Jahre werden mit dem gewählten Kalkulationszinssatz (drückt die Kosten des Kapitals aus) auf den gegenwertigen Zeitpunkt abgezinst/diskontiert. Daraus resultieren sogenannte Barwerte der Zahlungen. Der Netto-Kapitalwert sagt aus, was für den Kauf und den Betrieb der Anlage während der Betrachtungsperiode netto und unter Berücksichtigung der Kapitalkosten per heute in einem einzigen Betrag zu bezahlen wäre, bzw. was per heute verdient würde. Dieser Betrag ist eine mögliche Form, die wirtschaftliche Vorteilhaftigkeit eine Anlage auszudrücken. Er kann in seiner absoluten Höhe beurteilt oder mit alternativen Anlagen verglichen werden.
Formeln:
Einmalige Einnahmen:
Einnahmen Jahr 0 = Förderbeiträge einmalig + Steuererleichterung einmalig + Diverse Einnahmen einmalig + Kredit
\(B_{0} = B_{For,e} + B_{div,e} + B_{k}\)
Laufende Einnahmen:
Jährliche Einnahmen = Energieveräusserung * Energieverkaufspreis * Energiepreisteuerung + Förderbeiträge laufend + Diverse Einnahmen laufend + Verkauf thermische Energie * Energiepreisteuerung
\(B_{j} = E_{teg}*B_{En}*\left( 1 + e_{En} \right)^{j} + B_{For,\ c} + B_{div,\ \ c} + B_{En,\ \ therm\ }*\left( 1 + e_{En} \right)^{j} \)
Einmalige Ausgaben:
Anlagekosten = Investitionsausgaben für Bau
\(I_{0} = \sum_{k = 1}^{Anzahl\ Komp.}I_{k} \)
Einmalige Ausgaben = Anlagekosten + Tilgung + Diverse Ausgaben einmalig
\(A_{0} = I_{0} + A_{k} + A_{div,e} \)
Laufende Ausgaben:
Ersatzraten = Betrachtungsperiode / Lebensdauer
\(i_{m,k} = \left\lfloor \frac{n_{BP} – 1}{{\ n}_{tot,k}} \right\rfloor \) [1]
Ersatzentscheid ob eine Komponente ausgewechselt werden muss (0 = nein, 1 = ja)
\(a_{k,j} = left{ begin{matrix} 0, (j – 1) mod n_{tot,k} neq 0 \ 1, (j – 1) mod n_{tot,k} = 0 \ end{matrix} right. \) [2]
Ersatzinvestitionsausgaben pro Jahr = Investition * Ersatzentscheid * Preisänderung Ersatzbeschaffung
\(I_{m,j} = \sum_{k = 1}^{Anzahl\ Komp.}I_{k}*a_{k,j}*\left( 1 + e_{m} \right)^{j} \)
Jährliche Kosten = Wartung + Gebühren + Komponentenersatz pro Jahr + Energiebezug * Energiepreis * Energiepreisteuerung + max. Leistungsbezug * Leistungskosten * Energiepreisteuerung + Diverse Ausgaben
\(A_{j} = A_{OM} + A_{G}\ + I_{m,j} + {(E}_{eaux} + E_{Par})*A_{En}*{(1 + e_{En})}^{j} + max{(E}_{teg})*A_{P}*{(1 + e_{En})}^{j} + A_{div,c}\)
Restwert:
Restwert = Investitionsausgaben * Preisänderung Ersatzbeschaffung * lineare Abschreibung
\(W = (\ \sum_{k = 1}^{Anzahl\ Komp.}I_{k}*(1 + {e_{m})}^{i_{m,k}*n_{tot,k}}*\frac{\left( i_{m,k} + 1 \right)*n_{tot,k} – n_{BP}}{n_{tot,k}})\)
Netto Barwert:
\(NPV = \ B_{0} – A_{0} + W*\left( 1 + i_{i} \right)^{{- n}_{BP}}*\left( 1 + i_{r} \right)^{{- n}_{BP}}\ + \sum_{j = 1}^{n_{BP}}{(\left( B_{j} – A_{j} \right)*\left( 1 + i_{i} \right)^{- j} – A_{kr,j})*\left( 1 + i_{r} \right)^{- j}}\)
Die Kreditzinskosten werden nicht mit der Inflation indexiert. Weitere Informationen können dem Kapitel Begriffe der Wirtschaftlichkeit entnommen werden.
Zinssätze
Kalkulationszinssatz / Kapitalkostensatz
Der Kalkulationszinssatz wird dafür verwendet, die zu unterschiedlichen Zeitpunkten anfallenden zukünftigen Zahlungsströme bezüglich Zinsen vergleichbar zu machen. Die zukünftigen Einnahmen und Ausgaben werden mit diesem Zinssatz auf die Gegenwart abgezinst/diskontiert. Der Kalkulationszinssatz drückt die Kosten des Kapitals aus bzw. in Projekten mit einem Netto-Einnahmenüberschuss die erwartete Kapitalrendite.
Interner Zinssatz (IRR)
Die Methode des „internen Zinssatzes“, international auch Internal Rate of Return (IRR), oder der effektiven Verzinsung drückt die wirtschaftliche Vorteilhaftigkeit einer Investition als finanzmathematisch korrekt berechnete Rendite sämtlicher Zahlungsströme der Investition im gewählten Betrachtungszeitraum aus. Diese Rendite kann in ihrer absoluten Höhe beurteilt oder mit Alternativen verglichen werden. Während die Netto-Kapitalwertmethode von einem bestimmten Zinssatz (Kapitalkostensatz) ausgeht und damit den Netto-Barwert sämtlicher Zahlungen ermittelt, drückt der IRR jenen Zinssatz aus, bei welchem der Netto-Kapitalwert gleich null ist. Ein IRR wird sinnvoll berechnet, wenn im Betrachtungszeitraum die Summe sämtlicher Einnahmen grösser ist als die Summe sämtlicher Ausgaben (nur dann kann von einer Kapitalrendite gesprochen werden).
Der IRR ermöglicht es, für eine Investition oder Kapitalanlage, bei der unregelmäßige und schwanken- de Erträge anfallen, eine (theoretische) mittlere, jährliche Rendite zu berechnen. Ist der IRR negativ, so bedeutet dies, dass die Summe der finanziellen Rückflüsse kleiner ist als das eingesetzte Kapital.
Hier findet eine Gleichsetzung des NPV mit Null statt. Die Formel wird nach ir aufgelöst. Die Lösung für ir wird durch Iteration gefunden und entspricht dann dem IRR.

Amortisationszeit
Die Amortisationszeit berechnet die Zeit, während welcher die Investition betrieben werden muss, bis die Investitionsausgabe wieder mit Rückflüssen aus der Investition aufgefüllt ist. Eine Amortisationszeit gibt es für Investitionen, deren Rückflüsse bis zu einem bestimmten Zeitpunkt grösser oder gleich hoch wie die Investitionssumme sind.
Die einfache Amortisationsdauer kumuliert vom Beginn der Investition her alle Zahlungen in nomineller Höhe auf, bis der Kassenbestand wieder bei null steht.
Dynamische Amortisationsdauer
Die im WB-Tool verwendete dynamische Amortisationsdauer kumuliert vom Beginn der Investition her die Barwerte aller Zahlungen auf, bis der Netto-Kapitalwert wieder bei null steht. Die dynamische Amortisationsdauer drückt somit die Zeit aus, welche eine Investition betrieben werden muss, bis der zur Berechnung der Barwerte verwendete Zinssatz erreicht ist.
Annuität
Formeln:
\(AF = \frac{\left( 1 + i_{r} \right)^{n_{BP}}*i_{r}}{\left( 1 + i_{r} \right)^{n_{BP}} – 1} \)
Annuität = Kapitalwert * Annuitätsfaktor (AF)
\(A_{A} = NPV*AF \)
Inflation
Inflation bezeichnet eine allgemeine und anhaltende Erhöhung des Güterpreisniveaus, gleichbedeutend mit einer Minderung der Kaufkraft des Geldes. Gemessen wird die Inflation meist durch jährliche Preisänderungen von Gütern bestimmter Warenkörbe. Wie soll die erwartete Inflation in den erwarteten Zahlungsströmen einer Simulationsrechnung in Polysun berücksichtigt werden?
Im Falle von niedrigen erwarteten Inflationsraten ist von einen Inflationierung der zukünftigen Kosten und Erlöse aus folgenden Gründen dringend abzuraten:
Andere Einflüsse auf die Preise, wie z.B. die Angebots- / Nachfragesituation im Falle der Energiepreise, oder die Lebenszyklus-bedingten Preisänderung im Falle von energietechnischen Geräten, sind viel stärker als der Einfluss der Inflation.
Bei niedrigen Inflationsraten unterliegen die Wirtschaftssubjekte der sogenannten Geldillusion. Das Ausmass der Geldentwertung ist so klein und auf wenige Warengruppen beschränkt, dass Entscheide auf Grund von nominellen Preisen gefällt werden.
Die zukünftige Inflation in einer Volkswirtschaft ist auf lange Sicht nur mit relativ grosser Unsicherheit zu prognostizieren.
Im Währungsraum des Euro und des Schweizer Frankens ist die Inflation auf absehbare Zeit hinaus tief (Stand 2016). Im Falle von hohen erwarteten Inflationsraten (im Durchschnitt mehrerer Jahre über 5 °K) kann eine Inflationierung zukünftiger Preise und Kosten gerechtfertigt sein, weil dann auch die sogenannte Geldillusion der Wirtschaftssubjekte zerstört wird und die Mechanismen automatischer Indexierungen zu wirken beginnen. In einem solchen Fall gibt es im WB-Tool also die Möglichkeit, die erwarteten Einnahme und Ausgaben zu inflationieren.
Bei den Resultaten (auch in den Reports) werden alle Werte nominal (mit Inflation) angezeigt. Dies kann u.U. zu Verwirrung führen. Zum Beispiel dann wenn manuell gleichbleibende, jährliche Wartungskosten eingegeben werden und das Resultat für die gesamten Wartungskosten nicht dem multiplizierten Wert der Eingabe entspricht weil die Inflation den Wert beeinflusst. Anhand dieser Veränderung ist es aber möglich, den Einfluss der Inflation abschätzen zu können.
Kapitalkosten
Die Berechnung der wirtschaftlichen Vorteilhaftigkeit von Investitionsprojekten basiert grundsätzlich auf einem Gesamtkapital-Ansatz, weil die wirtschaftliche Leistungsfähigkeit einer Anlage nicht von ihrer Finanzierung abhängt. Der einzusetzende Kapitalkostensatz/Kalkulationszinssatz muss ein gewichteter durchschnittlicher Zinssatz aus Fremdkapital und Eigenkapital sein.[3]
Soll die wirtschaftliche Vorteilhaftigkeit der Investition unter Einschluss einer Kredit-Teilfinanzierung berechnet werden, so müssen sämtliche mit dem Kredit zusammenhängenden Einnahmen und Ausgaben (Kreditauszahlung = Einnahme, Kreditrückzahlung = Ausgabe, Zinszahlung = Ausgabe) erfasst werden. Die Einnahmen und Ausgaben eines Kredites werden durch das WB-Tool erfasst, wenn eine Kredit (Zinssatz, Summe, Laufzeit) definiert wird. Die Netto-Zahlungsströme sind dann nur noch durch Eigenkapital zu finanzieren. Der einzugebende Kalkulationszinssatz muss dann dem Eigenkapitalkostensatz bzw. im Falle von Projekten mit einem Netto-Einnahmenüberschuss der erwarteten Rendite auf das Eigenkapital entsprechen.
Im Falle eines Kredites (z.B. Bankkredit) rechnet das WB Tool automatisch eine Tilgung und berücksichtigt die entsprechenden Cashflows. Hierbei wird im Jahr Null die Kreditaufnahme als Einnahme und die spätere Tilgung als Ausgabe berücksichtigt. So ergibt sich rechnerisch ein „Nullsummenspiel“. Die Tilgungszahlungen werden in den Grafiken der Cash-Flow-Betrachtung angezeigt. Die Tilgung und die Zinskosten sind nicht dem Einfluss der Inflation unterworfen.
Energiegestehungskosten
Die Energiegestehungskosten geben die Kosten für eine bereitgestellte und nutzbare Energiemenge wieder. Bei der Berechnung der Energiegestehungskosten wird die Berechnungsmethode des LCOE[4] verwendet. Dabei werden die laufenden Kosten pro Betrachtungsjahr eruiert, über die Betrachtungsperiode aufsummiert und auf den Referenzzeitpunkt mit dem Kalkulationszinssatz diskontiert und die einmaligen Kosten hinzugerechnet. Die diskontierten Kosten werden durch die auf den Referenzzeitpunkt diskontierte, bereitgestellte und nutzbare Energiemenge dividiert. Der LCOE ist eine branchenübliche Berechnungsmethode für Stromgestehungskosten. Hier wird die Formel für die Berechnung der Gestehungskosten aller Energiearten zusammen, unabhängig ob thermisch oder elektrisch, angewandt.
Durch die Diskontierung aller Ausgaben und der erzeugten Energiemenge über die Betrachtungsperiode auf den gleichen Referenzpunkt wird die Vergleichbarkeit der Energiegestehungskosten gewährleistet. Die Energiegestehungskosten stellen eine Vergleichsrechnung nur auf Kostenbasis und nicht eine Berechnung der Höhe von Einspeisetarifen dar. Die Wertigkeit der jeweiligen Energiemenge wird und muss nicht separat berücksichtigt werden.
Formeln:
Energiegestehungskosten = diskontierte Kosten / diskontierte produzierte Energiemenge
\(G = \frac{A_{0} – W*\left( 1 + i_{r} \right)^{{- n}_{BP}}\left( 1 + i_{i} \right)^{{- n}_{BP}}\ + \sum_{j = 1}^{n_{BP}}{\left(A_{j}*\left( 1 + i_{i} \right)^{- j} + A_{kr,j} \right)*\left( 1 + i_{r} \right)^{- j}}}{\sum_{j = 1}^{n_{BP}}{\left( Q_{use,j} + Q_{inv,j} -Q_{Minderertrag\ PV,j} \right)*\left( 1 + i_{r} \right)^{- j}}} \)
Bei der Anteilberechnung über die Zusammensetzung der Energiebestehungskosten wird der Restwert den Ersatzinvestitionen in Abzug gebracht, die Kreditzinskosten werden bei Diverses mit berücksichtigt.
Kreditkosten
Die Kreditkosten (Fremdkapitalkosten) spiegeln die Zinskosten für einen Kredit zu nominellen Konditionen wider (nicht beeinflusst von Inflation). Je nach Tilgung unterscheiden sich die totalen Zinskosten. Für die Rückzahlung des Kredites kann zwischen drei Modellen gewählt werden:
Modell 1: Modell Annuität mit immer gleicher hoher Zahlung, welche aus abnehmenden Zinsanteilen und zunehmenden Amortisationsanteilen zusammengesetzt ist.

Formeln:
\(Annuit\ddot{a}t\ = \ Kreditsumme\ *\ \frac{(1 + Kreditzinssatz)^{Kreditlaufzeit}*Kreditzinssatz}{(1 + Kreditzinssatz)^{Kreditlaufzeit} – 1} \)
\(Tilgungsrate\ Jahr\ 1\ {(T}_{1}) = \ Annuit\ddot{a}t\ – \ Kreditsumme\ *\ Kreditzinssatz \)
\(Tilgungsrate\ (T_{t}) = \ T_{1}*{(1 + Kreditzinssatz)}^{Kreditlaufzeit\ – \ 1} \)
\(J\ddot{a}hrliche\ Zinskosten = \ Annuit\ddot{a}t\ – \ T_{t} \)
Modell 2: Konstante Teilamortisation (Tilgung) und abnehmende Zinszahlung
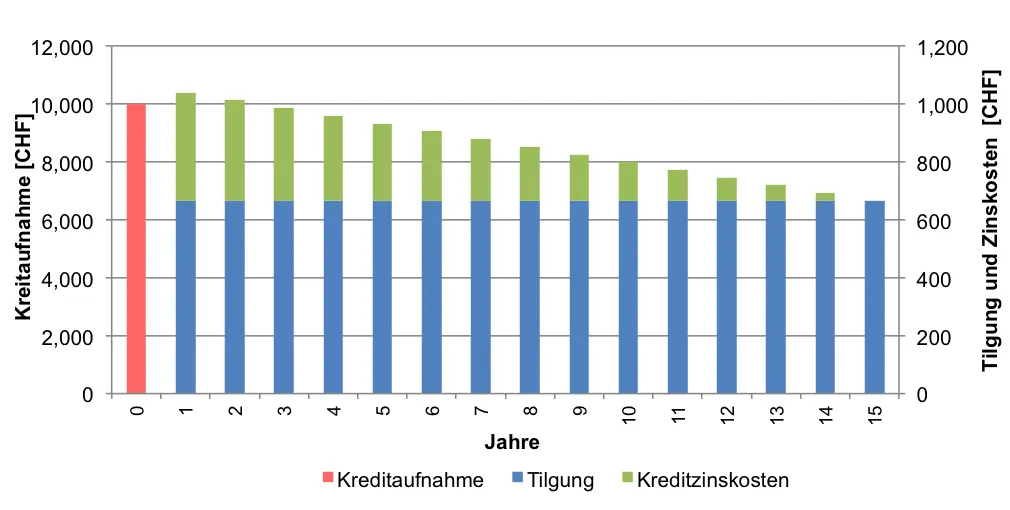
Formeln:
\(Tilgung\ = \ \frac{Kreditsumme\ }{Kreditlaufzeit} \)
\(Zinskosten\ = \ Kreditzinssatz\ *(Kreditsumme\ – \ \sum_{}^{}{geleistete\ Zinszahlungen}) \)
Modell 3: Festkredit (endfälliges Darlehen) mit Rückzahlung im letzten Jahr und jährlichen, gleichbleibenden Zinszahlungen
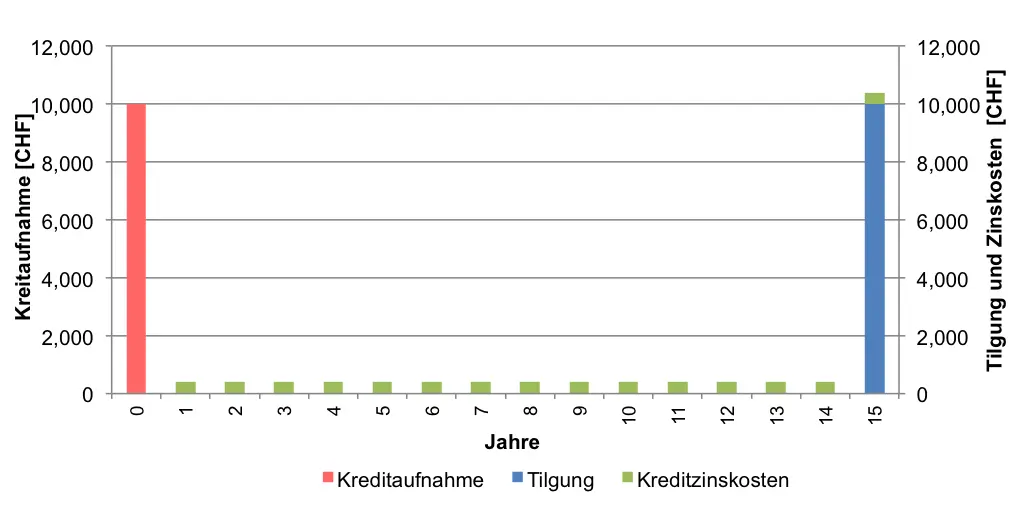
Formeln:
\(Zinskosten\ = \ Kreditzinssatz\ *Kreditsumme \)
Es ist bei der Eingabe jenes Modell zu wählen, welches dem eigenen Fall am ähnlichsten ist. In der Praxis wird das Annuitätsmodell relativ häufig angewandt.
Ersatzinvestitionen und technische Lebensdauer
Die technische Lebensdauer dient primär dazu, die Kosten für den Ersatz von Komponenten innerhalb der Betrachtungsperiode zu ermitteln und so eine Lebenszyklusanalyse in die Berechnung einzubringen. Weist eine Komponente z.B. eine halb so lange Lebensdauer auf als die Betrachtungsperiode lang ist, wird angenommen, dass die Komponente innerhalb der Betrachtungsperiode einmal ersetzt werden muss. Die Investitionsausgaben für diese Komponente verdoppeln sich entsprechend. Weist die (Rest)lebensdauer mehr Jahre aus als die (Rest)betrachtungsperiode, so entsteht nach Ablauf der Betrachtungsperiode ein Restwert, welcher in Abzug gebracht wird. Der Wertzerfall der Komponenten wird als linear angenommen. Die Preisänderungen im Zeitraum vom Referenzzeitpunkt bis zum Zeitpunkt eines Komponentenersatzes werden mit einem Faktor berücksichtigt. Dieser Faktor soll die Lernkurve für die Anschaffungspreise widerspiegeln und wird nach eigenem Ermessen eingegeben. Der Wert soll in Absprache mit der Bauherrschaft bestimmt oder aus verlässlichen Quellen übernommen werden. Wird der Wert positiv eingetragen, werden die Komponenten mit der Zeit teurer und umgekehrt.
Automatisierte Sensitivitätsanalyse
Die Genauigkeit des Resultats einer Wirtschaftlichkeitsberechnung ist stark von der Zuverlässigkeit der Eingabegrössen abhängig. Kleine Variationen in den Eingabegrössen können grosse Auswirkungen auf das Resultat haben. Es ist daher sinnvoll, bei Eingabegrössen mit grossem Einfluss eine Sensitivitätsanalyse bezüglich des Endresultates durchzuführen. Dabei wird die Wirtschaftlichkeitsberechnung mit den oberen und unteren Extremwerten für diese Eingabegrösse durchgeführt, während die anderen Eingabegrössen auf ihrem ursprünglichen Wert festgehalten werden. Mit der Sensitivitätsanalyse können Risiken und Chancen eines Projektes beurteilt werden.
Eingesparte Kosten durch PV
Die Ersparnis bei den Strombezugskosten wegen der durch die PV-Module erzeugten Energie wird mittels der laufenden Strombezugskosten errechnet. Dadurch können Sie klar erkennen, wie viel Sie für den extern bezogenen Strom würden bezahlen müssen, den Sie durch die PV-Module selbst erzeugen. Dieser Betrag zeigt, wie viel Geld der Eigentümer aufwenden müsste, wenn er kein PV-System installiert.
Die eingesparten Kosten durch Einsatz von PV werden wie folgt berechnet:
\(Q_{inv}(Stunde) – E_{teg}(Stunde)*Energiebezugstarif(Stunde) + E_{teg}(Stunde)*Einspeisungstarif(Stunde) \)
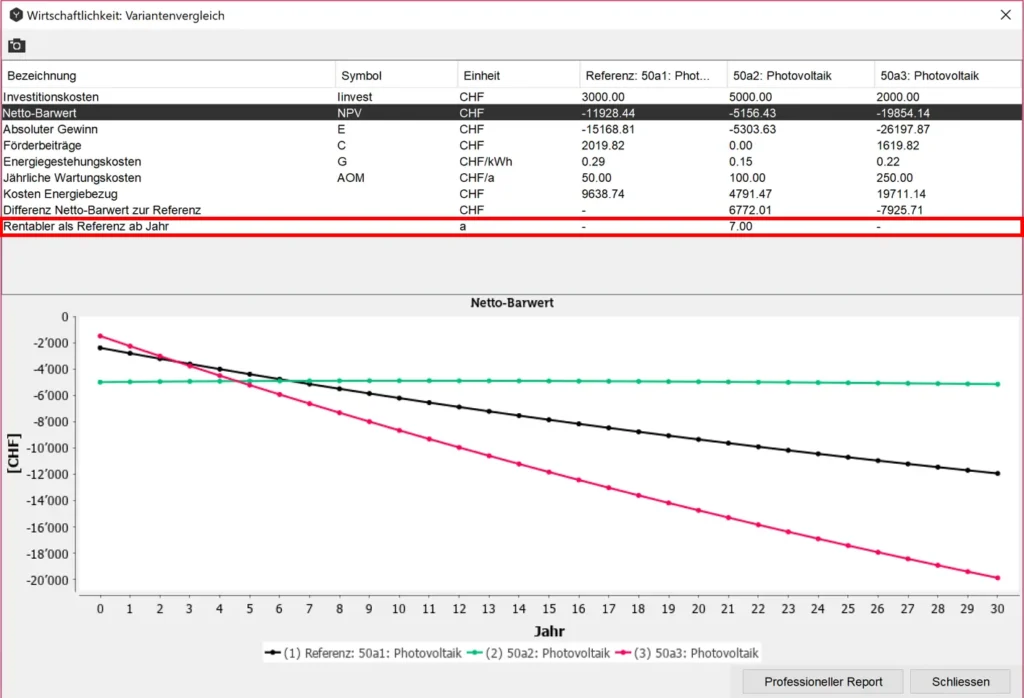
Rentabler als Referenz ab Jahr
Der Vergleich der Amortisationszeiträume für PV-Systeme zeigt, in welchem Jahr sich die Investition in ein PV-System bezahlt gemacht hat im Vergleich zu einem System ohne Photovoltaik-Einsatz. Mit anderen Worten: Das Jahr, in dem ein System mit Einsatz erneuerbarer Energie wirtschaftlicher wird als ein System mit konventioneller Energie. Wenn dieser Zeitpunkt nicht erreicht wird, wenn also der Einsatz der Photovoltaik im Vergleich zu einem konventionellen System wirtschaftlich keinen Sinn macht, erscheinen Striche an Stelle der Jahresangabe. In dem nachstehenden Beispiel ist das Projekt Nr. 3 (rote Linie) weniger wirtschaftlich als das System ohne PV (schwarze Linie), deshalb ist ein Bindestrich angegeben. Das Projekt Nr. 2 (grüne Linie) hat sich nach neun Jahren amortisiert.
[1] Die Abrundungsfunktion (Floor-Funktion) rundet auf die nächsttiefere ganze Zahl.
[2] Die mod-Funktion gibt den Wert nach dem Komma aus.
[3] Auch Eigenkapital verursacht Kosten, nämlich Opportunitätskosten in der Höhe der entgangenen Erträge, die mit einer alternativen Kapitalanlage möglich wären.
[4] Levelized Cost of Energy